4. Affordable and Clean Energy¶
Affordable and Clean Energy is the 7th Sustainable Development Goal 11. It aspires to ensure access to affordable, reliable, sustainable and modern energy for all. Today renewable energy is making impressive gains in the electricity sector. As more and more new settlements are built, there would be new electricity distribution network developed. Electricity Distribution is very expensive infrastructure. Finding the optimal path for laying this infrastructure is very crucial to maintain the affordability of electricity for everyone. This exercise focusses on finding this optimal path/network for laying the electricity distribution equipment.
4.1. Problem: Optimising the Electricity Distribution Network¶
Problem Statement
To determine the least length of the path for laying the electricity distribution equipment such that every building is served
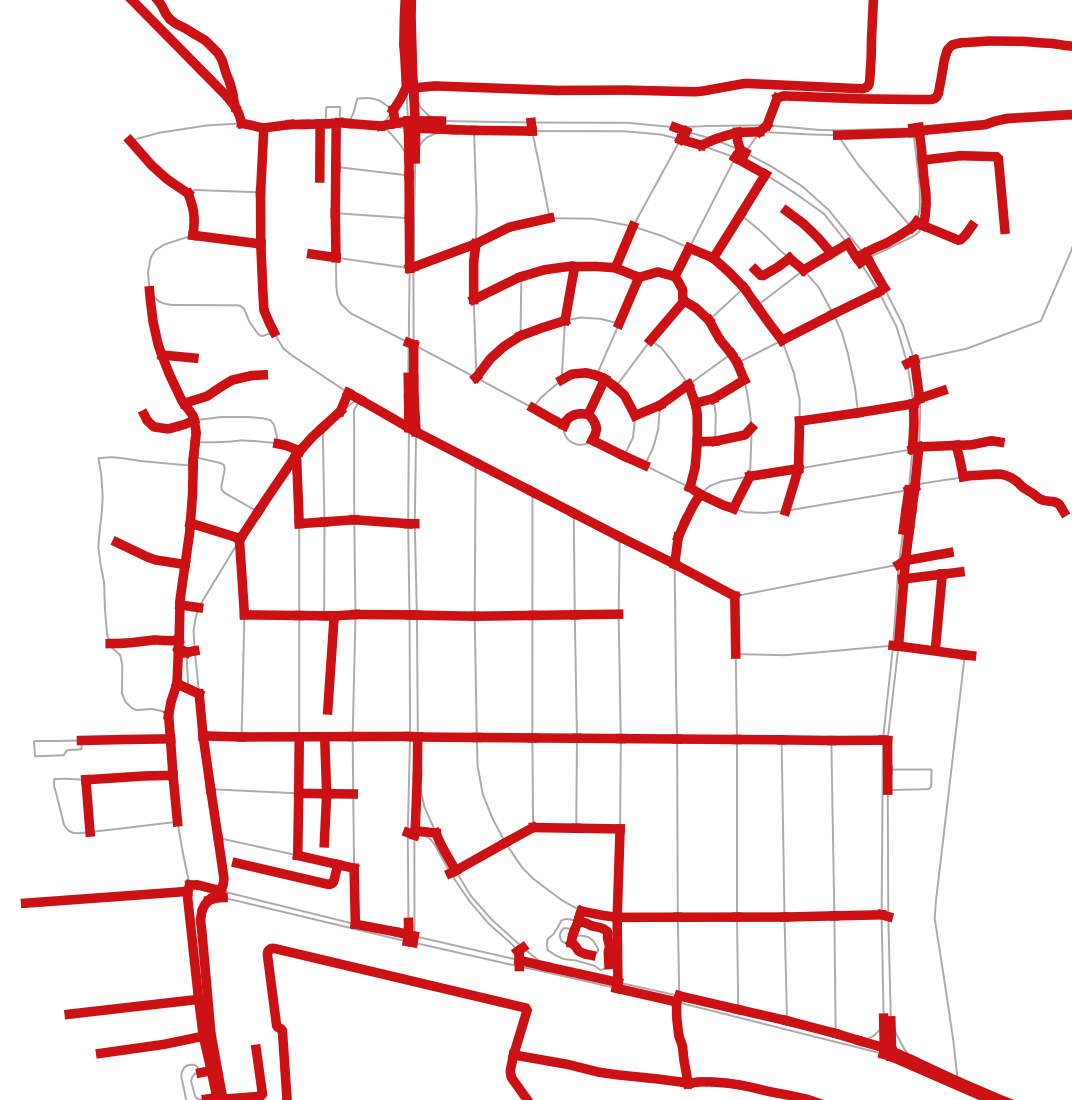
Core Idea
Electricity lines may not be there on every road of the city. In a complex road network of a city, the network can be optimised for less length such that Electricity lines reach every locality of the city. Less length leads to enhanced cost-effectiveness resulting in affordable electricity.
Approach
Extract connected components of roads
Use pgRouting to find the minimum spanning tree
Compare the total length of roads and minimum spanning tree
4.2. Pre-processing roads data¶
First step is to pre-process the data obtained from Data for Sustainable Development Goals. This section will work the graph that is going to be used for processing. While building the graph, the data has to be inspected to determine if there is any invalid data. This is a very important step to make sure that the data is of required quality. pgRouting can also be used to do some Data Adjustments. This will be discussed in further sections.
4.2.1. Setting the Search Path of Roads¶
First step in pre processing is to set the search path for Roads data.
Search path is a list of schemas helps the system determine how a particular table
is to be imported.
4.2.1.1. Exercise 1: Set the seach path¶
In this case, search path of roads table is search path to roads and
buildings schemas. Following query is used to adjust the search path.
SET search_path TO roads,public,contrib,postgis;
SET
Checking the search path again
SHOW search_path;
search_path
---------------------------------
roads, public, contrib, postgis
(1 row)
4.2.1.2. Exercise 2: Remove disconnected components¶
To remove the disconnected components on the road network, the following pgRouting functions, discussed on Graph views, will be used:
pgr_extractVerticespgr_connectedComponents
Create a vertices table.
SELECT * INTO roads.roads_vertices
FROM pgr_extractVertices(
'SELECT gid AS id, source, target
FROM roads.roads_ways ORDER BY id');
SELECT 378
Fill up the x, y and geom columns.
UPDATE roads_vertices SET geom = ST_startPoint(the_geom)
FROM roads_ways WHERE source = id;
UPDATE roads_vertices SET geom = ST_endPoint(the_geom)
FROM roads_ways WHERE geom IS NULL AND target = id;
UPDATE roads_vertices set (x,y) = (ST_X(geom), ST_Y(geom));
UPDATE 349
UPDATE 29
UPDATE 378
Add a component column on the edges and vertices tables.
ALTER TABLE roads_ways ADD COLUMN component BIGINT;
ALTER TABLE roads_vertices ADD COLUMN component BIGINT;
ALTER TABLE
ALTER TABLE
Fill up the component column on the vertices table.
UPDATE roads_vertices SET component = c.component
FROM (
SELECT * FROM pgr_connectedComponents(
'SELECT gid as id, source, target, cost, reverse_cost FROM roads_ways')
) AS c
WHERE id = node;
UPDATE 378
Fill up the component column on the edges table.
UPDATE roads_ways SET component = v.component
FROM (SELECT id, component FROM roads_vertices) AS v
WHERE source = v.id;
UPDATE 558
Get the component number with the most number of edges.
WITH
all_components AS (SELECT component, count(*) FROM roads_ways GROUP BY component),
max_component AS (SELECT max(count) from all_components)
SELECT component FROM all_components WHERE count = (SELECT max FROM max_component);
component
-----------
1
(1 row)
Delete edges not belonging to the most connected component.
WITH
all_components AS (SELECT component, count(*) FROM roads_ways GROUP BY component),
max_component AS (SELECT max(count) from all_components),
the_component AS (SELECT component FROM all_components WHERE count = (SELECT max FROM max_component))
DELETE FROM roads_ways WHERE component != (SELECT component FROM the_component);
DELETE 0
Delete vertices not belonging to the most connected component.
WITH
all_components AS (SELECT component, count(*) FROM roads_vertices GROUP BY component),
max_component AS (SELECT max(count) from all_components),
the_component AS (SELECT component FROM all_components WHERE count = (SELECT max FROM max_component))
DELETE FROM roads_vertices WHERE component != (SELECT component FROM the_component);
DELETE 0
4.3. pgr_kruskalDFS¶
For the next step pgr_kruskalDFS will be used. Kruskal algorithm is used for
getting the Minimum Spanning Tree with Depth First Search ordering. A minimum spanning
tree (MST) is a subset of edges of a connected undirected graph that connects all
the vertices together, without any cycles such that sum of edge weights is as small
as possible.
Signatures
pgr_kruskalDFS(Edges SQL, Root vid [, max_depth])
pgr_kruskalDFS(Edges SQL, Root vids [, max_depth])
RETURNS SET OF (seq, depth, start_vid, node, edge, cost, agg_cost)
pgr_kruskalDFS Documentation can be found at this link for more information.
4.4. Exercise 3: Find the minimum spanning tree¶
The road network has a minimum spanning forest which is a union of the minimum spanning trees for its connected components. This minimum spanning forest is the optimal network of electricity distribution components.
To complete this task, execute the query below.
PREPARE edges AS
SELECT gid AS id, source, target, length_m AS cost
FROM roads.roads_ways;
PREPARE
The following query will give the results with the source vertex, target vertex, edge id, aggregate cost.
SELECT seq, depth, start_vid, node, edge, round(cost::numeric, 2) AS length, round(agg_cost::numeric, 2) AS agg_cost
FROM pgr_kruskalDFS('edges', 91);
seq | depth | start_vid | node | edge | length | agg_cost
-----+-------+-----------+------+------+---------+----------
1 | 0 | 91 | 91 | -1 | 0.00 | 0.00
2 | 1 | 91 | 77 | 151 | 12.78 | 12.78
3 | 2 | 91 | 24 | 127 | 74.05 | 86.83
4 | 3 | 91 | 92 | 153 | 10.60 | 97.43
5 | 4 | 91 | 316 | 480 | 57.61 | 155.03
6 | 5 | 91 | 260 | 479 | 51.99 | 207.02
7 | 6 | 91 | 247 | 381 | 177.65 | 384.67
8 | 5 | 91 | 292 | 443 | 68.48 | 223.51
9 | 4 | 91 | 82 | 133 | 65.95 | 163.37
10 | 5 | 91 | 228 | 357 | 37.86 | 201.24
11 | 6 | 91 | 227 | 356 | 32.42 | 233.66
12 | 7 | 91 | 93 | 154 | 49.84 | 283.50
13 | 8 | 91 | 111 | 155 | 68.57 | 352.07
14 | 8 | 91 | 373 | 551 | 29.72 | 313.22
15 | 9 | 91 | 371 | 550 | 2.14 | 315.36
16 | 9 | 91 | 374 | 552 | 59.79 | 373.01
17 | 10 | 91 | 372 | 549 | 27.54 | 400.54
18 | 10 | 91 | 375 | 1 | 117.03 | 490.04
19 | 9 | 91 | 157 | 258 | 109.54 | 422.75
20 | 10 | 91 | 13 | 259 | 8.35 | 431.10
21 | 10 | 91 | 213 | 342 | 103.40 | 526.16
22 | 11 | 91 | 364 | 541 | 10.51 | 536.66
23 | 8 | 91 | 37 | 62 | 12.24 | 295.74
24 | 5 | 91 | 38 | 65 | 10.31 | 173.68
25 | 6 | 91 | 224 | 64 | 34.38 | 208.06
26 | 7 | 91 | 223 | 353 | 31.11 | 239.17
27 | 2 | 91 | 58 | 126 | 86.93 | 99.71
28 | 3 | 91 | 51 | 95 | 91.31 | 191.02
29 | 4 | 91 | 23 | 37 | 77.16 | 268.18
30 | 5 | 91 | 81 | 132 | 71.51 | 339.69
31 | 5 | 91 | 22 | 38 | 76.12 | 344.30
32 | 6 | 91 | 314 | 34 | 58.04 | 402.34
33 | 7 | 91 | 21 | 31 | 56.31 | 458.65
34 | 8 | 91 | 20 | 33 | 19.38 | 478.03
35 | 9 | 91 | 70 | 29 | 75.15 | 553.18
36 | 10 | 91 | 69 | 114 | 62.95 | 616.14
37 | 11 | 91 | 68 | 113 | 31.76 | 647.89
38 | 12 | 91 | 72 | 111 | 55.17 | 703.07
39 | 13 | 91 | 56 | 117 | 41.91 | 744.98
40 | 14 | 91 | 55 | 92 | 56.01 | 801.00
41 | 15 | 91 | 71 | 91 | 21.09 | 822.09
42 | 16 | 91 | 54 | 116 | 14.19 | 836.28
43 | 17 | 91 | 53 | 90 | 57.17 | 893.45
44 | 16 | 91 | 360 | 115 | 62.74 | 884.83
45 | 17 | 91 | 25 | 536 | 46.43 | 931.25
46 | 18 | 91 | 52 | 42 | 55.88 | 987.14
47 | 17 | 91 | 361 | 537 | 47.13 | 931.96
48 | 18 | 91 | 57 | 93 | 55.25 | 987.21
49 | 19 | 91 | 19 | 28 | 35.29 | 1022.50
50 | 11 | 91 | 73 | 120 | 29.00 | 645.14
51 | 12 | 91 | 33 | 55 | 56.63 | 701.77
52 | 13 | 91 | 276 | 54 | 29.19 | 730.97
53 | 14 | 91 | 32 | 423 | 17.79 | 748.76
54 | 15 | 91 | 31 | 53 | 64.65 | 813.41
55 | 16 | 91 | 30 | 51 | 49.91 | 863.31
56 | 17 | 91 | 29 | 50 | 43.36 | 906.67
57 | 18 | 91 | 28 | 48 | 58.10 | 964.77
58 | 19 | 91 | 27 | 47 | 39.39 | 1004.16
59 | 20 | 91 | 46 | 80 | 72.58 | 1076.74
60 | 20 | 91 | 75 | 45 | 63.20 | 1067.36
61 | 21 | 91 | 26 | 123 | 84.34 | 1151.70
62 | 22 | 91 | 16 | 44 | 82.58 | 1234.27
63 | 23 | 91 | 15 | 24 | 90.98 | 1325.26
64 | 24 | 91 | 6 | 23 | 103.92 | 1429.17
65 | 25 | 91 | 174 | 12 | 5.97 | 1435.15
66 | 26 | 91 | 282 | 432 | 81.24 | 1516.39
67 | 27 | 91 | 280 | 428 | 69.45 | 1585.84
68 | 28 | 91 | 250 | 384 | 27.65 | 1613.49
69 | 29 | 91 | 176 | 293 | 49.30 | 1662.78
70 | 30 | 91 | 8 | 294 | 11.03 | 1673.81
71 | 31 | 91 | 257 | 394 | 49.71 | 1723.52
72 | 31 | 91 | 249 | 13 | 58.70 | 1732.52
73 | 32 | 91 | 14 | 383 | 31.49 | 1764.01
74 | 33 | 91 | 62 | 21 | 89.74 | 1853.75
75 | 34 | 91 | 84 | 102 | 13.97 | 1867.72
76 | 30 | 91 | 211 | 339 | 11.76 | 1674.55
77 | 31 | 91 | 83 | 135 | 10.93 | 1685.48
78 | 32 | 91 | 278 | 426 | 40.57 | 1726.05
79 | 32 | 91 | 277 | 134 | 41.67 | 1727.15
80 | 33 | 91 | 353 | 424 | 11.84 | 1738.99
81 | 34 | 91 | 203 | 525 | 1282.14 | 3021.13
82 | 34 | 91 | 352 | 524 | 1053.24 | 2792.23
83 | 31 | 91 | 368 | 338 | 20.42 | 1694.96
84 | 32 | 91 | 256 | 547 | 22.36 | 1717.32
85 | 33 | 91 | 366 | 543 | 50.49 | 1767.81
86 | 34 | 91 | 230 | 359 | 13.76 | 1781.56
87 | 35 | 91 | 18 | 27 | 5.14 | 1786.71
88 | 36 | 91 | 279 | 427 | 70.75 | 1857.45
89 | 37 | 91 | 281 | 430 | 75.25 | 1932.71
90 | 38 | 91 | 295 | 447 | 72.28 | 2004.98
91 | 39 | 91 | 283 | 433 | 37.86 | 2042.85
92 | 36 | 91 | 231 | 361 | 16.59 | 1803.30
93 | 37 | 91 | 345 | 514 | 8.22 | 1811.52
94 | 38 | 91 | 344 | 513 | 87.90 | 1899.42
95 | 38 | 91 | 222 | 351 | 23.47 | 1834.99
96 | 39 | 91 | 221 | 350 | 23.12 | 1858.11
97 | 40 | 91 | 9 | 15 | 40.80 | 1898.91
98 | 41 | 91 | 192 | 319 | 104.72 | 2003.63
99 | 42 | 91 | 193 | 320 | 83.92 | 2087.54
100 | 43 | 91 | 285 | 436 | 146.33 | 2233.87
101 | 43 | 91 | 190 | 315 | 105.70 | 2193.24
102 | 44 | 91 | 138 | 225 | 69.06 | 2262.30
103 | 45 | 91 | 191 | 316 | 124.94 | 2387.24
104 | 41 | 91 | 114 | 187 | 34.94 | 1933.85
105 | 42 | 91 | 242 | 186 | 29.07 | 1962.92
106 | 43 | 91 | 113 | 375 | 531.95 | 2494.88
107 | 43 | 91 | 243 | 374 | 265.65 | 2228.57
108 | 32 | 91 | 367 | 546 | 21.71 | 1716.67
109 | 33 | 91 | 273 | 419 | 42.71 | 1759.38
110 | 34 | 91 | 12 | 18 | 1282.70 | 3042.08
111 | 24 | 91 | 45 | 78 | 122.20 | 1447.46
112 | 19 | 91 | 66 | 46 | 81.13 | 1045.90
113 | 20 | 91 | 65 | 108 | 85.11 | 1131.01
114 | 21 | 91 | 64 | 106 | 73.36 | 1204.37
115 | 22 | 91 | 63 | 105 | 96.45 | 1300.81
116 | 23 | 91 | 17 | 25 | 1.22 | 1302.04
117 | 18 | 91 | 47 | 82 | 51.32 | 957.99
118 | 19 | 91 | 48 | 83 | 40.71 | 998.70
119 | 20 | 91 | 76 | 124 | 67.69 | 1066.39
120 | 21 | 91 | 49 | 84 | 35.49 | 1101.88
121 | 22 | 91 | 50 | 86 | 68.06 | 1169.95
122 | 23 | 91 | 59 | 97 | 89.80 | 1259.75
123 | 24 | 91 | 40 | 67 | 79.21 | 1338.95
124 | 25 | 91 | 89 | 147 | 10.39 | 1349.34
125 | 26 | 91 | 355 | 146 | 54.76 | 1404.10
126 | 27 | 91 | 88 | 529 | 9.03 | 1413.13
127 | 28 | 91 | 198 | 324 | 85.23 | 1498.35
128 | 29 | 91 | 313 | 475 | 12.34 | 1510.69
129 | 30 | 91 | 356 | 474 | 11.93 | 1522.62
130 | 31 | 91 | 197 | 531 | 91.63 | 1614.25
131 | 31 | 91 | 354 | 530 | 107.02 | 1629.64
132 | 32 | 91 | 209 | 527 | 235.79 | 1865.43
133 | 32 | 91 | 357 | 526 | 46.68 | 1676.33
134 | 33 | 91 | 219 | 533 | 299.95 | 1976.28
135 | 34 | 91 | 95 | 159 | 6.74 | 1983.02
136 | 35 | 91 | 96 | 160 | 189.17 | 2172.19
137 | 34 | 91 | 220 | 348 | 322.95 | 2299.23
138 | 33 | 91 | 351 | 532 | 6.70 | 1683.03
139 | 34 | 91 | 210 | 523 | 9.06 | 1692.09
140 | 35 | 91 | 217 | 337 | 6.76 | 1698.85
141 | 36 | 91 | 272 | 417 | 116.92 | 1815.77
142 | 27 | 91 | 362 | 538 | 12.65 | 1416.75
143 | 28 | 91 | 363 | 540 | 9.27 | 1426.02
144 | 29 | 91 | 41 | 69 | 26.88 | 1452.90
145 | 30 | 91 | 275 | 70 | 29.61 | 1482.50
146 | 31 | 91 | 60 | 422 | 50.73 | 1533.23
147 | 32 | 91 | 304 | 461 | 28.94 | 1562.17
148 | 33 | 91 | 305 | 462 | 66.95 | 1629.12
149 | 31 | 91 | 274 | 421 | 98.36 | 1580.86
150 | 20 | 91 | 61 | 101 | 82.37 | 1081.07
151 | 21 | 91 | 42 | 71 | 75.53 | 1156.60
152 | 22 | 91 | 43 | 74 | 53.96 | 1210.57
153 | 23 | 91 | 87 | 143 | 14.61 | 1225.18
154 | 24 | 91 | 194 | 321 | 8.45 | 1233.63
155 | 24 | 91 | 218 | 141 | 29.48 | 1254.66
156 | 25 | 91 | 86 | 139 | 37.28 | 1291.94
157 | 26 | 91 | 94 | 156 | 22.36 | 1314.30
158 | 27 | 91 | 44 | 75 | 33.53 | 1347.83
159 | 28 | 91 | 85 | 138 | 15.55 | 1363.37
160 | 29 | 91 | 206 | 137 | 18.66 | 1382.03
161 | 25 | 91 | 269 | 347 | 34.35 | 1289.01
162 | 26 | 91 | 294 | 445 | 15.51 | 1304.52
163 | 27 | 91 | 195 | 322 | 46.99 | 1351.51
164 | 28 | 91 | 196 | 323 | 536.21 | 1887.72
165 | 17 | 91 | 67 | 49 | 82.39 | 945.70
166 | 10 | 91 | 74 | 121 | 27.79 | 580.97
167 | 11 | 91 | 34 | 56 | 62.07 | 643.04
168 | 8 | 91 | 80 | 32 | 48.31 | 506.96
169 | 9 | 91 | 79 | 130 | 29.20 | 536.17
170 | 10 | 91 | 306 | 129 | 44.12 | 580.29
171 | 11 | 91 | 112 | 463 | 106.68 | 686.97
172 | 12 | 91 | 293 | 444 | 94.00 | 780.97
173 | 11 | 91 | 131 | 213 | 95.61 | 675.90
174 | 12 | 91 | 127 | 206 | 80.79 | 756.69
175 | 13 | 91 | 123 | 200 | 72.61 | 829.30
176 | 14 | 91 | 267 | 408 | 99.58 | 928.88
177 | 15 | 91 | 3 | 5 | 104.85 | 1033.72
178 | 16 | 91 | 175 | 7 | 13.05 | 1046.77
179 | 17 | 91 | 226 | 355 | 47.70 | 1094.47
180 | 18 | 91 | 229 | 358 | 34.22 | 1128.69
181 | 17 | 91 | 122 | 292 | 87.95 | 1134.72
182 | 18 | 91 | 141 | 199 | 21.47 | 1156.19
183 | 19 | 91 | 121 | 230 | 32.00 | 1188.19
184 | 20 | 91 | 332 | 197 | 38.04 | 1226.23
185 | 21 | 91 | 302 | 500 | 52.26 | 1278.50
186 | 22 | 91 | 140 | 458 | 8.12 | 1286.61
187 | 23 | 91 | 119 | 194 | 112.06 | 1398.68
188 | 24 | 91 | 333 | 502 | 39.07 | 1437.75
189 | 25 | 91 | 270 | 414 | 46.09 | 1483.84
190 | 26 | 91 | 183 | 304 | 83.53 | 1567.37
191 | 27 | 91 | 120 | 195 | 10.21 | 1577.58
192 | 23 | 91 | 347 | 228 | 110.06 | 1396.67
193 | 24 | 91 | 330 | 517 | 51.35 | 1448.02
194 | 25 | 91 | 147 | 496 | 2.52 | 1450.54
195 | 26 | 91 | 108 | 242 | 121.99 | 1572.54
196 | 27 | 91 | 150 | 180 | 84.65 | 1657.19
197 | 28 | 91 | 334 | 247 | 38.45 | 1695.64
198 | 29 | 91 | 338 | 503 | 15.53 | 1711.17
199 | 30 | 91 | 148 | 507 | 33.03 | 1744.20
200 | 31 | 91 | 182 | 244 | 83.45 | 1827.66
201 | 32 | 91 | 106 | 303 | 11.38 | 1839.04
202 | 33 | 91 | 103 | 177 | 89.23 | 1928.27
203 | 34 | 91 | 124 | 171 | 89.21 | 2017.47
204 | 35 | 91 | 128 | 201 | 65.47 | 2082.94
205 | 36 | 91 | 107 | 208 | 67.74 | 2150.68
206 | 30 | 91 | 337 | 506 | 153.06 | 1864.23
207 | 25 | 91 | 329 | 494 | 81.22 | 1529.24
208 | 26 | 91 | 189 | 495 | 93.46 | 1622.70
209 | 27 | 91 | 346 | 516 | 14.51 | 1637.21
210 | 28 | 91 | 301 | 456 | 23.70 | 1660.91
211 | 29 | 91 | 289 | 439 | 36.21 | 1697.12
212 | 30 | 91 | 288 | 440 | 90.02 | 1787.14
213 | 30 | 91 | 290 | 441 | 32.02 | 1729.14
214 | 31 | 91 | 291 | 442 | 133.29 | 1862.42
215 | 31 | 91 | 286 | 437 | 85.89 | 1815.03
216 | 32 | 91 | 287 | 438 | 49.60 | 1864.63
217 | 32 | 91 | 284 | 434 | 106.35 | 1921.38
218 | 26 | 91 | 336 | 505 | 67.85 | 1597.10
219 | 27 | 91 | 335 | 504 | 112.53 | 1709.63
220 | 27 | 91 | 208 | 335 | 66.09 | 1663.19
221 | 28 | 91 | 300 | 455 | 56.10 | 1719.29
222 | 29 | 91 | 299 | 454 | 107.13 | 1826.42
223 | 29 | 91 | 137 | 224 | 14.32 | 1733.61
224 | 30 | 91 | 136 | 222 | 57.83 | 1791.44
225 | 31 | 91 | 135 | 219 | 52.98 | 1844.42
226 | 32 | 91 | 134 | 220 | 38.34 | 1882.76
227 | 33 | 91 | 376 | 554 | 137.56 | 2020.32
228 | 33 | 91 | 328 | 218 | 59.58 | 1942.34
229 | 34 | 91 | 235 | 493 | 75.73 | 2018.08
230 | 34 | 91 | 377 | 556 | 134.79 | 2077.13
231 | 35 | 91 | 378 | 557 | 85.08 | 2162.20
232 | 31 | 91 | 322 | 221 | 4.87 | 1796.31
233 | 32 | 91 | 321 | 486 | 14.72 | 1811.02
234 | 33 | 91 | 325 | 485 | 9.17 | 1820.20
235 | 34 | 91 | 204 | 490 | 9.23 | 1829.42
236 | 35 | 91 | 100 | 165 | 68.41 | 1897.83
237 | 36 | 91 | 117 | 191 | 87.50 | 1985.33
238 | 37 | 91 | 116 | 190 | 79.93 | 2065.26
239 | 38 | 91 | 161 | 265 | 87.65 | 2152.91
240 | 39 | 91 | 184 | 306 | 22.71 | 2175.62
241 | 40 | 91 | 10 | 307 | 21.76 | 2197.38
242 | 40 | 91 | 327 | 492 | 329.88 | 2505.50
243 | 41 | 91 | 326 | 491 | 138.44 | 2643.94
244 | 41 | 91 | 1 | 2 | 771.94 | 3277.44
245 | 39 | 91 | 185 | 264 | 48.61 | 2201.52
246 | 40 | 91 | 241 | 308 | 10.66 | 2212.18
247 | 41 | 91 | 240 | 373 | 176.36 | 2388.54
248 | 42 | 91 | 239 | 372 | 60.26 | 2448.79
249 | 43 | 91 | 234 | 371 | 161.04 | 2609.84
250 | 43 | 91 | 308 | 370 | 57.13 | 2505.93
251 | 44 | 91 | 307 | 467 | 45.00 | 2550.93
252 | 45 | 91 | 309 | 468 | 16.30 | 2567.24
253 | 44 | 91 | 310 | 466 | 16.35 | 2522.28
254 | 42 | 91 | 188 | 312 | 201.35 | 2589.89
255 | 41 | 91 | 187 | 311 | 251.03 | 2463.21
256 | 36 | 91 | 152 | 166 | 59.45 | 1957.28
257 | 37 | 91 | 151 | 251 | 89.19 | 2046.47
258 | 38 | 91 | 149 | 250 | 82.41 | 2128.88
259 | 39 | 91 | 181 | 245 | 88.83 | 2217.71
260 | 40 | 91 | 97 | 301 | 11.70 | 2229.42
261 | 41 | 91 | 238 | 369 | 63.01 | 2292.43
262 | 42 | 91 | 237 | 367 | 89.67 | 2382.10
263 | 43 | 91 | 173 | 289 | 32.44 | 2414.54
264 | 44 | 91 | 172 | 286 | 68.23 | 2482.77
265 | 45 | 91 | 178 | 285 | 9.33 | 2492.10
266 | 45 | 91 | 105 | 287 | 89.02 | 2571.79
267 | 46 | 91 | 126 | 174 | 49.50 | 2621.29
268 | 47 | 91 | 130 | 212 | 66.62 | 2687.91
269 | 48 | 91 | 133 | 217 | 67.74 | 2755.65
270 | 49 | 91 | 102 | 169 | 143.72 | 2899.37
271 | 50 | 91 | 165 | 273 | 105.77 | 3005.14
272 | 51 | 91 | 164 | 272 | 114.14 | 3119.28
273 | 52 | 91 | 268 | 270 | 42.39 | 3161.67
274 | 53 | 91 | 177 | 411 | 10.18 | 3171.85
275 | 53 | 91 | 315 | 477 | 15.27 | 3176.93
276 | 54 | 91 | 171 | 478 | 9.92 | 3186.85
277 | 51 | 91 | 317 | 482 | 9.70 | 3014.84
278 | 52 | 91 | 236 | 481 | 95.50 | 3110.34
279 | 53 | 91 | 166 | 274 | 10.73 | 3121.07
280 | 54 | 91 | 167 | 276 | 93.83 | 3214.90
281 | 55 | 91 | 168 | 278 | 77.52 | 3292.42
282 | 56 | 91 | 169 | 280 | 77.94 | 3370.36
283 | 57 | 91 | 156 | 256 | 39.26 | 3409.62
284 | 58 | 91 | 170 | 282 | 39.36 | 3448.98
285 | 59 | 91 | 11 | 283 | 9.98 | 3458.96
286 | 60 | 91 | 359 | 17 | 12.22 | 3471.19
287 | 61 | 91 | 7 | 535 | 255.17 | 3726.35
288 | 61 | 91 | 160 | 534 | 9.06 | 3480.24
289 | 62 | 91 | 153 | 263 | 48.84 | 3529.08
290 | 62 | 91 | 154 | 253 | 37.11 | 3517.35
291 | 63 | 91 | 212 | 341 | 76.59 | 3593.94
292 | 64 | 91 | 216 | 344 | 183.54 | 3777.48
293 | 59 | 91 | 155 | 255 | 48.28 | 3497.27
294 | 53 | 91 | 271 | 365 | 134.61 | 3244.95
295 | 54 | 91 | 233 | 416 | 273.94 | 3518.89
296 | 55 | 91 | 365 | 542 | 2463.71 | 5982.60
297 | 55 | 91 | 358 | 363 | 633.79 | 4152.69
298 | 54 | 91 | 232 | 362 | 450.74 | 3695.69
299 | 50 | 91 | 104 | 173 | 56.27 | 2955.63
300 | 51 | 91 | 202 | 330 | 16.95 | 2972.58
301 | 52 | 91 | 266 | 406 | 19.76 | 2992.33
302 | 53 | 91 | 200 | 326 | 17.35 | 3009.69
303 | 54 | 91 | 199 | 327 | 38.30 | 3047.99
304 | 52 | 91 | 201 | 328 | 103.81 | 3076.38
305 | 50 | 91 | 110 | 170 | 93.70 | 2993.07
306 | 51 | 91 | 144 | 184 | 91.44 | 3084.51
307 | 52 | 91 | 143 | 236 | 73.38 | 3157.90
308 | 53 | 91 | 142 | 233 | 77.03 | 3234.93
309 | 54 | 91 | 35 | 232 | 72.99 | 3307.92
310 | 55 | 91 | 159 | 58 | 10.75 | 3318.67
311 | 43 | 91 | 2 | 3 | 7.25 | 2389.35
312 | 44 | 91 | 186 | 310 | 11.11 | 2400.46
313 | 41 | 91 | 101 | 162 | 91.40 | 2320.82
314 | 42 | 91 | 125 | 167 | 85.79 | 2406.61
315 | 43 | 91 | 129 | 203 | 68.87 | 2475.48
316 | 44 | 91 | 132 | 209 | 67.74 | 2543.21
317 | 45 | 91 | 109 | 214 | 86.94 | 2630.15
318 | 46 | 91 | 145 | 181 | 92.57 | 2722.72
319 | 47 | 91 | 99 | 238 | 68.88 | 2791.61
320 | 48 | 91 | 98 | 164 | 76.77 | 2868.38
321 | 49 | 91 | 36 | 163 | 79.74 | 2948.12
322 | 50 | 91 | 158 | 60 | 7.22 | 2955.34
323 | 51 | 91 | 312 | 473 | 47.17 | 3002.50
324 | 52 | 91 | 311 | 471 | 33.39 | 3035.89
325 | 38 | 91 | 118 | 192 | 91.98 | 2138.45
326 | 39 | 91 | 341 | 510 | 43.22 | 2181.67
327 | 40 | 91 | 339 | 509 | 81.76 | 2263.43
328 | 40 | 91 | 340 | 508 | 79.97 | 2261.64
329 | 40 | 91 | 331 | 497 | 41.03 | 2222.70
330 | 39 | 91 | 146 | 240 | 100.84 | 2239.29
331 | 40 | 91 | 343 | 239 | 63.81 | 2303.10
332 | 41 | 91 | 115 | 512 | 25.70 | 2328.80
333 | 42 | 91 | 162 | 267 | 90.85 | 2419.65
334 | 43 | 91 | 179 | 297 | 65.89 | 2485.54
335 | 44 | 91 | 163 | 269 | 17.76 | 2503.29
336 | 45 | 91 | 349 | 520 | 8.95 | 2512.25
337 | 46 | 91 | 348 | 518 | 10.46 | 2522.71
338 | 47 | 91 | 350 | 522 | 8.71 | 2531.42
339 | 45 | 91 | 180 | 299 | 20.22 | 2523.51
340 | 41 | 91 | 342 | 511 | 184.06 | 2487.16
341 | 30 | 91 | 320 | 223 | 5.08 | 1738.69
342 | 31 | 91 | 324 | 484 | 8.92 | 1747.61
343 | 32 | 91 | 323 | 488 | 7.10 | 1754.71
344 | 33 | 91 | 205 | 487 | 6.23 | 1760.94
345 | 28 | 91 | 139 | 226 | 29.01 | 1692.20
346 | 22 | 91 | 303 | 457 | 35.78 | 1314.28
347 | 16 | 91 | 225 | 6 | 52.94 | 1086.67
348 | 17 | 91 | 4 | 354 | 33.39 | 1120.06
349 | 18 | 91 | 5 | 8 | 55.42 | 1175.48
350 | 19 | 91 | 207 | 9 | 8.29 | 1183.78
351 | 1 | 91 | 90 | 150 | 62.73 | 62.73
352 | 2 | 91 | 39 | 149 | 12.26 | 74.99
353 | 1 | 91 | 78 | 128 | 38.03 | 38.03
(353 rows)
4.5. Comparison between Total and Optimal lengths¶
Total lengths of the network and the minimum spanning tree can be compared to see the difference between both. To do the same, follow the steps below:
4.5.1. Exercise 4: Compute total length of material required in km¶
Compute the total length of the minimum spanning tree which is an estimate of the total length of material required.
1SELECT sum(cost)/1000 AS material_km
2FROM pgr_kruskalDFS('edges', 91);
material_km
--------------------
29.889909026094898
(1 row)
4.5.2. Exercise 5: Compute total length of roads¶
Compute the total length of the road network of the given area..
SELECT sum(length_m)/1000 AS total_km
FROM roads_ways;
total_km
-------------------
55.68114222824193
(1 row)
-For this area we are getting following outputs:
-
-* Total Road Length: 55.68 km
-* Optimal Network Length: 29.89 km
Length of minimum spanning tree is about half of the length of total road network.
4.6. Further possible extensions to the exercise¶
Find the optimal network of roads such that it reaches every building
Find the optimal number and locations of Electricity Transformers