2. Enrutamiento peatonal

pgRouting se llamó por primera vez pgDijkstra, porque implementó sólo la búsqueda de ruta más corta con el algoritmo Dijkstra. Más tarde se agregaron otras funciones y se cambió el nombre de la biblioteca a pgRouting.

2.1. pgr_dijkstra

El algoritmo Dijkstra fue el primer algoritmo implementado en pgRouting. No requiere otros atributos que no sean id, source y target ID y cost y reverse_cost.

Puede especificar cuándo considerar el grafo como dirigido o sin dirección.

Resumen de funciones

pgr_dijkstra(Edges SQL, start_vid,  end_vid  [, directed])
pgr_dijkstra(Edges SQL, start_vid,  end_vids [, directed])
pgr_dijkstra(Edges SQL, start_vids, end_vid  [, directed])
pgr_dijkstra(Edges SQL, start_vids, end_vids [, directed])
pgr_dijkstra(Edges SQL, Combinations SQL [, directed])

RETURNS SET OF (seq, path_seq [, start_vid] [, end_vid], node, edge, cost, agg_cost)
    OR EMPTY SET

La descripción de los parámetros se puede encontrar en pgr_dijkstra.

Nota

• Muchas funciones pgRouting tienen sql::text como uno de sus argumentos. Aunque esto puede parecer confuso al principio, hace que las funciones sean muy flexibles, ya que el usuario puede pasar una instrucción SELECT como argumento de función siempre y cuando el resultado devuelto contenga el número necesario de atributos y los nombres de atributo correctos.

• La mayoría de los algoritmos implementados pgRouting no requieren la geometría.

• Las funciones pgRouting no devuelven una geometría, sino solo una lista ordenada de nodos o aristas.

Identificadores de las consultas

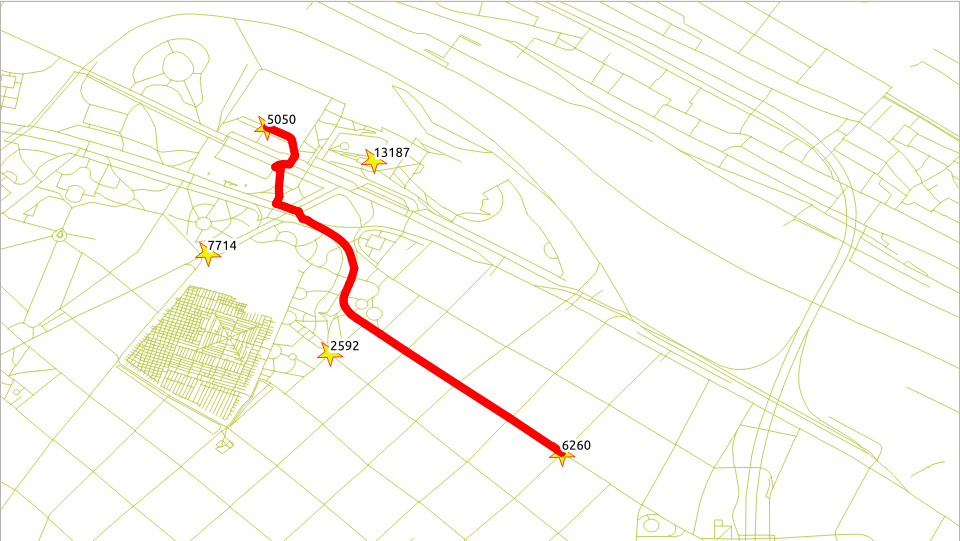
La asignación de los identificadores de vértices en las columnas de origen y destino puede ser diferentes, los siguientes ejercicios usarán los resultados de esta consulta. Para el taller, se van a utilizar algunos lugares cercanos al evento FOSS4G Argentina. Estas ubicaciones se encuentran dentro de esta área https://www.openstreetmap.org#map=15/-34.5847/-58.3970

• 192903446 Plaza Intendente Alvear

• 4289340366 Hard Rock Café

• 2153015792 Facultad de Derecho

• 6357258588 Centro de Convenciones Buenos Aires

• 196017392 Palacio Duhau-Park Hyatt Buenos Aires

Conéctese a la base de datos, si no está conectado:

psql city_routing

Obtener los identificadores de vértice

SELECT osm_id, id FROM ways_vertices_pgr
WHERE osm_id IN (192903446, 4289340366, 2153015792, 6357258588, 196017392)
ORDER BY osm_id;

   osm_id   |  id   
------------+-------
  192903446 |  1993
  196017392 |  2197
 2153015792 |  6646
 4289340366 |  9129
 6357258588 | 15011
(5 rows)

• 192903446 Plaza Intendente Alvear (1993)

• 4289340366 Hard Rock Café (9129)

• 2153015792 Facultad de Derecho (6646)

• 6357258588 Centro de Convenciones Buenos Aires (15011)

• 196017392 Palacio Duhau-Park Hyatt Buenos Aires (2197)

El correspondiente id se muestra en la siguiente imagen y una ruta de ejemplo de «Facultad de Derecho» a «Palacio Duhau-Park Hyatt Buenos Aires».

2.1.1. Ejercicio 1: Ruteo para un solo peatón

Problema:

• Caminando de «Plaza Intendente Alvear» al «Facultad de Derecho».

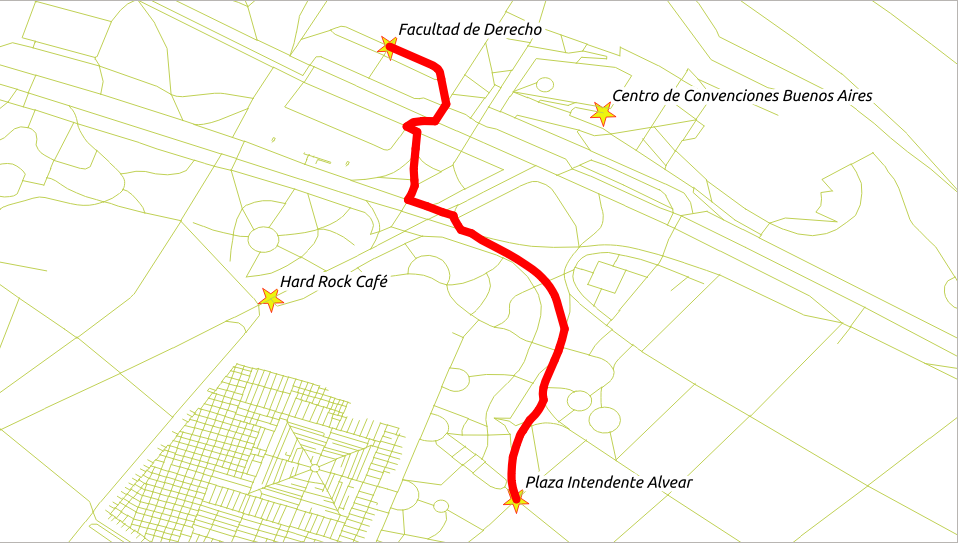
Solución:

• El peatón quiere pasar del vértice 1993 al vértice 6646 (líneas 9 y 10).

• El costo del peatón es en términos de longitud. En este caso length (línea 6), que fue calculada por osm2pgrouting, está en la unidad degrees.

• Desde una perspectiva peatonal, el grafo es no dirigido (línea 11), es decir, el peatón puede moverse en ambas direcciones en todos los segmentos.

SELECT * FROM pgr_dijkstra(
    '
      SELECT gid AS id,
        source,
        target,
        length AS cost
      FROM ways
    ',
 1993,
 6646,
    directed := false);

Ejercicio: 1 (Capítulo: Peatón)

Nota

• El atributo cost devuelto representa el costo especificado en la consulta SQL interna (edges_sql::text argument). En este ejemplo, el costo es length en la unidad «degrees». El costo puede ser tiempo, distancia o cualquier combinación de ambos o cualquier otro atributo o una fórmula personalizada.

• Los resultados de node y edge pueden variar dependiendo de la asignación de los identificadores a los vértices dados por osm2pgrouting.

2.1.2. Ejercicio 2: Muchos peatones van al mismo destino

Problema:

• Caminando desde «Plaza Intendente Alvear» y «Hard Rock Café» hasta «Facultad de Derecho».

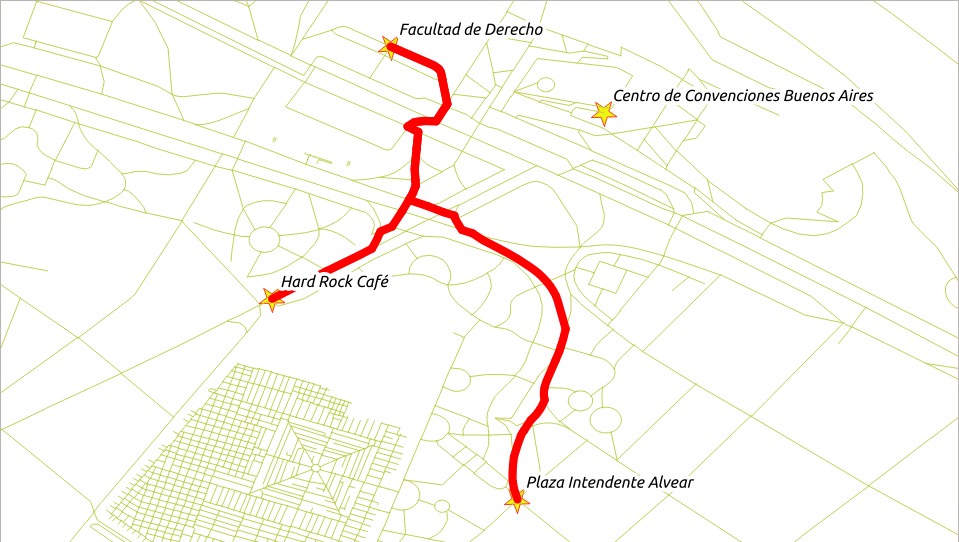
Solución:

• Los peatones están saliendo en los vértices 1993 y 9129 (línea 9).

• Todos los peatones quieren ir al vértice 6646 (línea 10).

• El costo de estar en metros usando el atributo length_m (línea 6).

SELECT * FROM pgr_dijkstra(
    '
      SELECT gid AS id,
        source,
        target,
        length_m AS cost
      FROM ways
    ',
ARRAY[1993,9129],
6646,
directed := false);

Ejercicio: 2 (Capítulo: Peatón)

2.1.3. Ejercicio 3: Muchos peatones que salen de la misma ubicación

Problema:

• Caminando desde «Facultad de Derecho» hasta «Plaza Intendente Alvear» y «Hard Rock Café» (en segundos).

Solución:

• Todos los peatones están saliendo del vértice 6646 (línea 9).

• Los peatones quieren ir a lugares 1993 y 9129 (línea 10).

• El costo a ser en segundos, con una velocidad de marcha s = 1.3 m/s y t = d/s (línea 6).

SELECT * FROM pgr_dijkstra(
    '
      SELECT gid AS id,
        source,
        target,
        length_m / 1.3 AS cost
      FROM ways
    ',
6646,
ARRAY[1993,9129],
directed := false);

Ejercicio: 3 (Capítulo: Peatón)

2.1.4. Ejercicio 4: Muchos peatones que van a diferentes destinos

Problema:

• Caminando desde los hoteles hasta «Centro de Convenciones Buenos Aires» y «Palacio Duhau-Park Hyatt Buenos Aires» (en minutos).

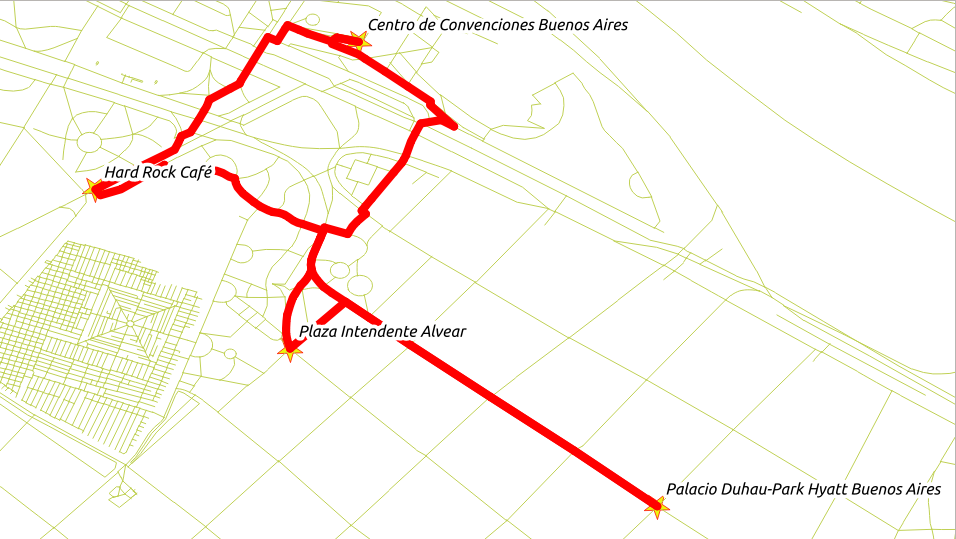
Solución:

• Los peatones parten de 1993 y 9129 (línea 9).

• Los peatones quieren ir a destinos 15011 y 2197 (línea 10).

• El costo a ser en minutos, con una velocidad de caminata s = 1.3 m/s y t = d/s (línea 6).

• El resultado suma los costes por destino.

SELECT * FROM pgr_dijkstra(
    '
      SELECT gid AS id,
       source,
       target,
       length_m / 1.3 / 60 AS cost
      FROM ways
    ',
ARRAY[1993, 9129],
ARRAY[15011, 2197],
directed := false);

Ejercicio: 4 (Capítulo: Peatón)

Nota

Inspección de los resultados, buscando totales (edge = -1):

• Ir a vértice 15011:

  • desde 1993 toma 8.84.. minutos (seq = 35)

  • desde 9129 toma 5.84.. minutos (seq = 74)

• Ir a vértice 2197:

  • desde 1993 toma 7.44.. minutos (seq = 7)

  • desde 9129 toma 12.06.. minutos (seq = 55)

2.2. pgr_dijkstraCost

Cuando el objetivo principal es calcular el costo total, sin «inspeccionar» los resultados de la pgr_dijkstra usando pgr_dijkstraCost devuelve un resultado más compacto.

Resumen de funciones

pgr_dijkstraCost(edges_sql, start_vid,  end_vid  [, directed])
pgr_dijkstraCost(edges_sql, start_vid,  end_vids [, directed])
pgr_dijkstraCost(edges_sql, start_vids, end_vid  [, directed])
pgr_dijkstraCost(edges_sql, start_vids, end_vids [, directed])
pgr_dijkstraCost(edges_sql, combinations_sql   [, directed])

RETURNS SET OF (start_vid, end_vid, agg_cost)
    OR EMPTY SET

La descripción de los parámetros se puede encontrar en pgr_dijkstraCost

2.2.1. Ejercicio 5: Muchos peatones que van a diferentes destinos devolviendo costos agregados

Problema:

• Caminando desde los hoteles hasta el «Centro de Convenciones Buenos Aires» o «Palacio Duhau-Park Hyatt Buenos Aires» (obtener sólo el costo en minutos).

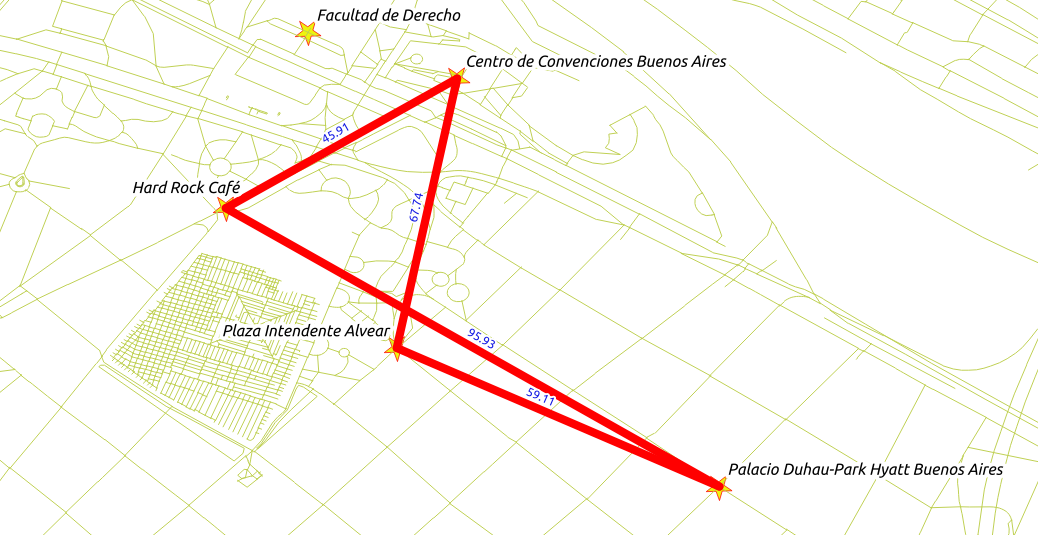
Solución:

• Los peatones parten de 1993 y 9129 (línea 10).

• Los peatones quieren ir a destinos 15011 y 2197 (línea 11).

• El costo a ser en minutos, con una velocidad de caminata s = 1.3 m/s y t = d/s (línea 7).

• Resultado como costos agregados.

SELECT *
FROM pgr_dijkstraCost(
    '
      SELECT gid AS id,
       source,
       target,
       length_m  / 1.3 / 60 AS cost
      FROM ways
    ',
ARRAY[1993, 9129],
ARRAY[15011, 2197],
directed := false);

Ejercicio: 5 (Capítulo: Peatón)

Compare with Exercise 4: Many Pedestrians going to different destinations “s note.

2.2.2. Ejercicio 6: Muchos peatones van a diferentes destinos resumiendo costos totales por salida

Problema:

• Caminando desde los hoteles hasta el «Centro de Convenciones Buenos Aires» o «Palacio Duhau-Park Hyatt Buenos Aires» (resumir el costo en minutos).

Solución:

• Los peatones parten de 1993 y 9129 (línea 10).

• Los peatones quieren ir a destinos 15011 y 2197 (línea 11).

• El costo a ser en minutos, con una velocidad de caminata s = 1.3 m/s y t = d/s (línea 7).

• El resultado suma los costes por destino.

SELECT start_vid, sum(agg_cost)
FROM pgr_dijkstraCost(
    '
      SELECT gid AS id,
        source,
        target,
        length_m  / 1.3 / 60 AS cost
      FROM ways
    ',
    ARRAY[1993, 9129],
    ARRAY[15011, 2197],
    directed := false)
GROUP BY start_vid
ORDER BY start_vid;

Ejercicio: 6 (Capítulo: Peatón)

Nota

Una interpretación del resultado puede ser: En general, es más rápido apartarse de la «Hard Rock Café» que de la «Plaza Intendente Alvear».