2. Pedestrian Routing ¶

pgRouting was first called pgDijkstra, because it implemented only shortest path search with Dijkstra algorithm. Later other functions were added and the library was renamed to pgRouting.

2.1. pgr_dijkstra ¶

Dijkstra algorithm was the first algorithm implemented in pgRouting. It doesn’t require other attributes than the identifiers id, source and target and the weights cost and reverse_cost.

You can specify when to consider the graph as directed or undirected.

Signature Summary

pgr_dijkstra(Edges SQL, start_vid,  end_vid  [, directed])
pgr_dijkstra(Edges SQL, start_vid,  end_vids [, directed])
pgr_dijkstra(Edges SQL, start_vids, end_vid  [, directed])
pgr_dijkstra(Edges SQL, start_vids, end_vids [, directed])
pgr_dijkstra(Edges SQL, Combinations SQL [, directed])

RETURNS SET OF (seq, path_seq [, start_vid] [, end_vid], node, edge, cost, agg_cost)
    OR EMPTY SET

Description of the parameters can be found in pgr_dijkstra.

Note

Many pgRouting functions have sql::text as one of their arguments. While this may look confusing at first, it makes the functions very flexible as the user can pass a SELECT statement as function argument as long as the returned result contains the required number of attributes and the correct attribute names.
Most of pgRouting implemented algorithms do not require the geometry.
The pgRouting functions do not return a geometry, but only an ordered list of nodes or edges.

Identifiers for the Queries

The assignment of the vertices identifiers on the source and target columns may be different, the following exercises will use the results of this query. For the workshop, some locations near of the FOSS4G event are going to be used. These locations are within this area https://www.openstreetmap.org#map=15/-34.5847/-58.3970

2385630446 Nadir Xhemali Danijolli
1838481592 Qendra Sprotive
1840522495 Kalaja e Prizrenit
6917727056 Inovation and Training Park
2385655026 Lidhja Shqiptare e Prizrenit

Connect to the database, if not connected:

psql city_routing

Get the vertex identifiers

SELECT osm_id, id FROM ways_vertices_pgr
WHERE osm_id IN (2385630446, 1838481592, 1840522495, 6917727056, 2385655026)
ORDER BY osm_id;

   osm_id   |  id  
------------+------
 1838481592 | 2592
 1840522495 | 2820
 2385630446 | 3770
 2385655026 | 3829
 6917727056 | 5912
(5 rows)

2385630446 Nadir Xhemali Danijolli (3770)
1838481592 Qendra Sprotive (2592)
1840522495 Kalaja e Prizrenit (2820)
6917727056 Inovation and Training Park (5912)
2385655026 Lidhja Shqiptare e Prizrenit (3829)

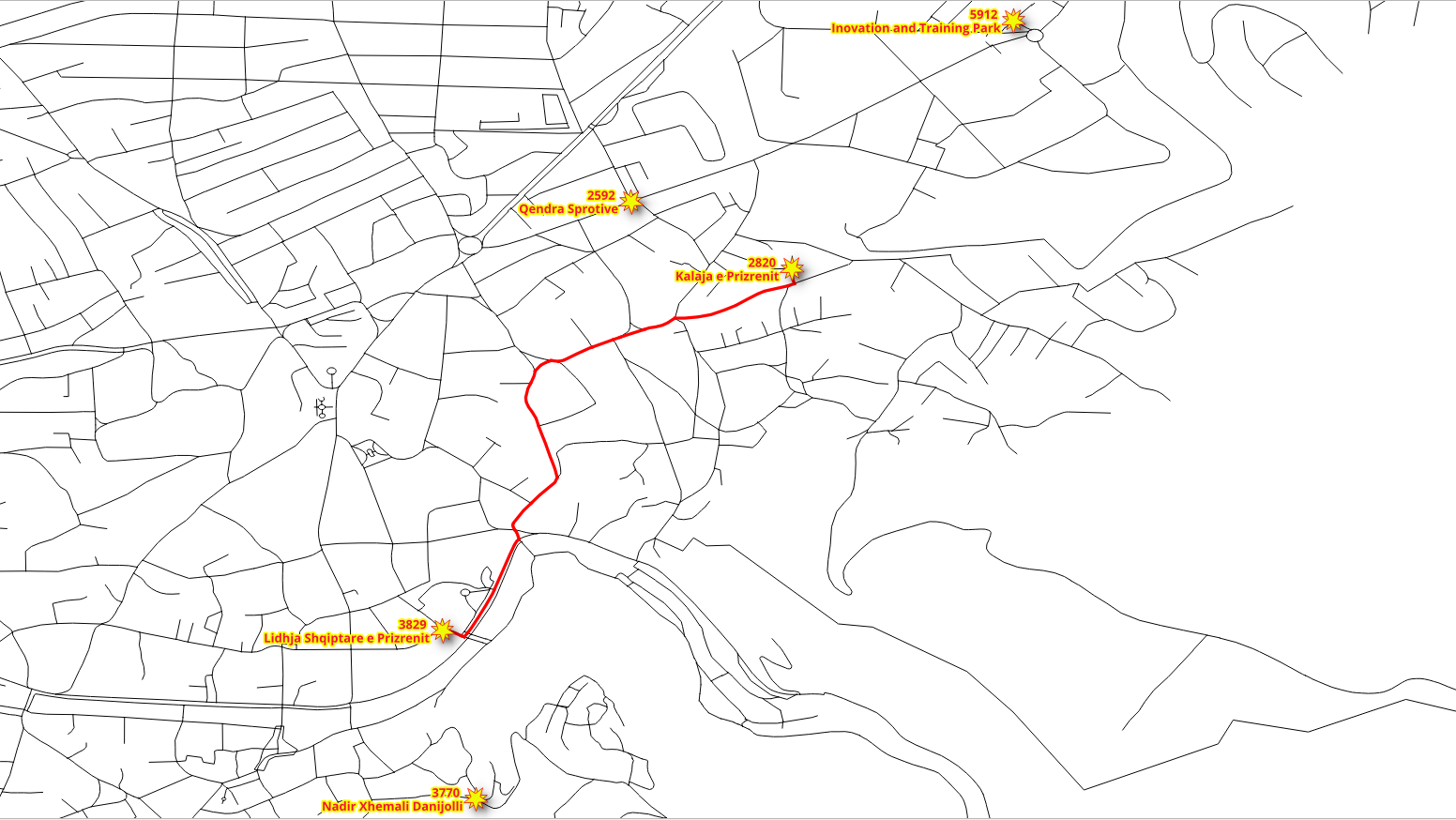
The corresponding id are shown in the following image, and a sample route from “Kalaja e Prizrenit” to “Lidhja Shqiptare e Prizrenit”.

2.1.1. Exercise 1: Single pedestrian routing ¶

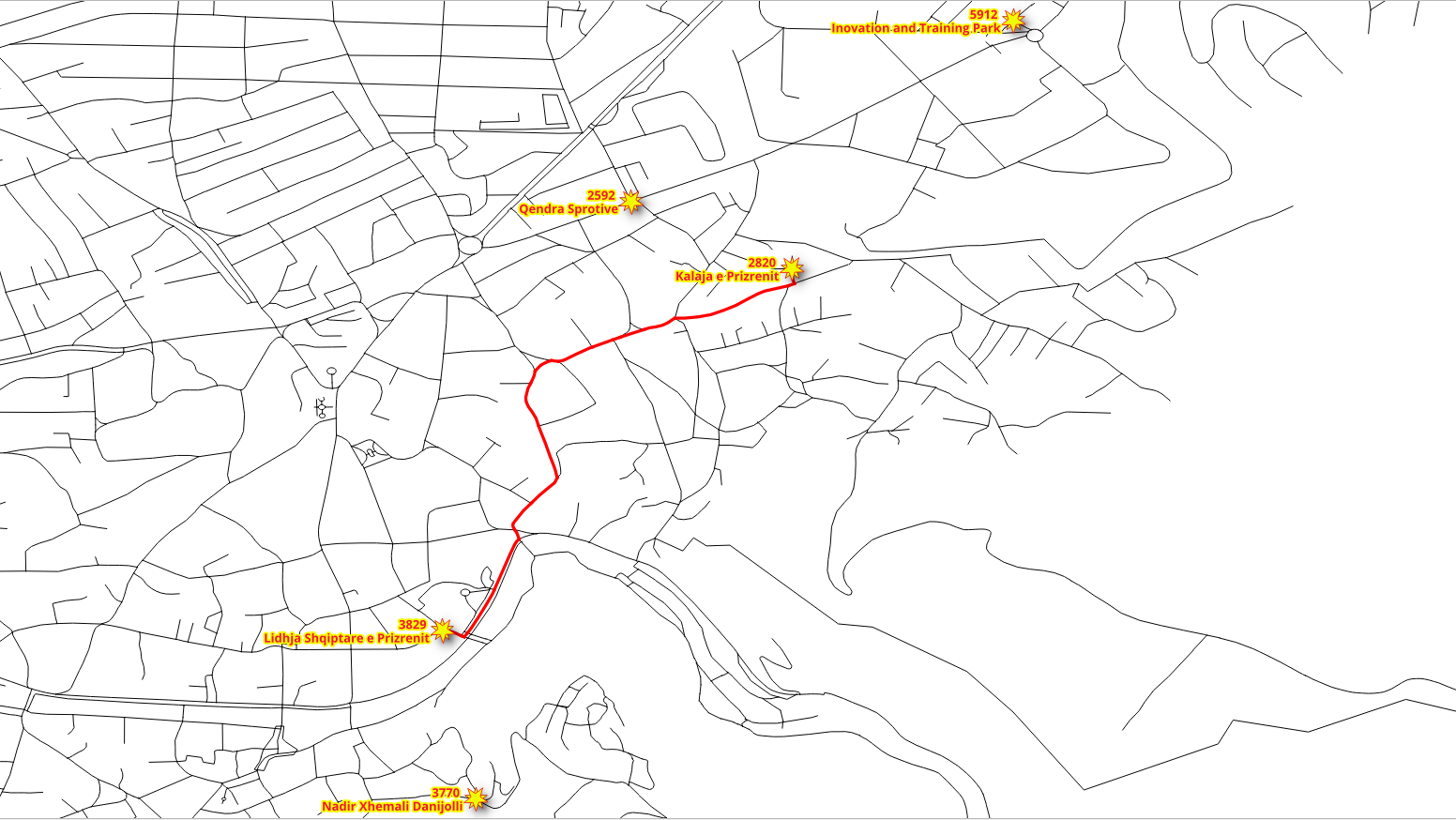
Problem:

Walking
- from “Nadir Xhemali Danijolli”
- to “Kalaja e Prizrenit”.
Calculate routes with costs in osm2pgRouting length default units.

Solution:

The pedestrian wants to go from vertex 3770 to vertex 2820 (lines 9 and 10).
The pedestrian’s cost is in terms of length. In this case length (line 6), which was calculated by osm2pgrouting, is in unit degrees.
From a pedestrian perspective the graph is undirected (line 11), that is, the pedestrian can move in both directions on all segments.

SELECT * FROM pgr_dijkstra(
    '
      SELECT gid AS id,
        source,
        target,
        length AS cost
      FROM ways
    ',
 3770,
 2820,
    directed := false);

Exercise: 1 (Chapter: Pedestrian)

Note

The returned cost attribute represents the cost specified in the inner SQL query (edges_sql::text argument). In this example cost is length in unit “degrees”. Cost may be time, distance or any combination of both or any other attributes or a custom formula.
node and edge results may vary depending on the assignment of the identifiers to the vertices given by osm2pgrouting.

2.1.2. Exercise 2: Many Pedestrians going to the same destination ¶

Problem:

Walking
- from “Nadir Xhemali Danijolli” and “Qendra Sprotive”
- to the “Kalaja e Prizrenit”.
Calculate routes with costs in osm2pgRouting length_m which is in meters.

From |place_1| and |place_2| to |place_3|

Solution:

The pedestrians are departing at vertices 3770 and 2592 (line 9).
All pedestrians want to go to vertex 2820 (line 10).
The cost to be in meters using attribute length_m (line 6).

SELECT * FROM pgr_dijkstra(
    '
      SELECT gid AS id,
        source,
        target,
        length_m AS cost
      FROM ways
    ',
ARRAY[3770,2592],
2820,
directed := false);

Exercise: 2 (Chapter: Pedestrian)

2.1.3. Exercise 3: Many Pedestrians departing from the same location ¶

Problem:

Walking
- from “Kalaja e Prizrenit”
- to “Nadir Xhemali Danijolli” and “Qendra Sprotive”
Calculate routes with costs in seconds.

Solution:

All pedestrians are departing from vertex 2820 (line 9).
Pedestrians want to go to locations 3770 and 2592 (line 10).
The cost to be in seconds, with a walking speed s = 1.3 m/s and t = d/s (line 6).

SELECT * FROM pgr_dijkstra(
    '
      SELECT gid AS id,
        source,
        target,
        length_m / 1.3 AS cost
      FROM ways
    ',
2820,
ARRAY[3770,2592],
directed := false);

Exercise: 3 (Chapter: Pedestrian)

2.1.4. Exercise 4: Many Pedestrians going to different destinations ¶

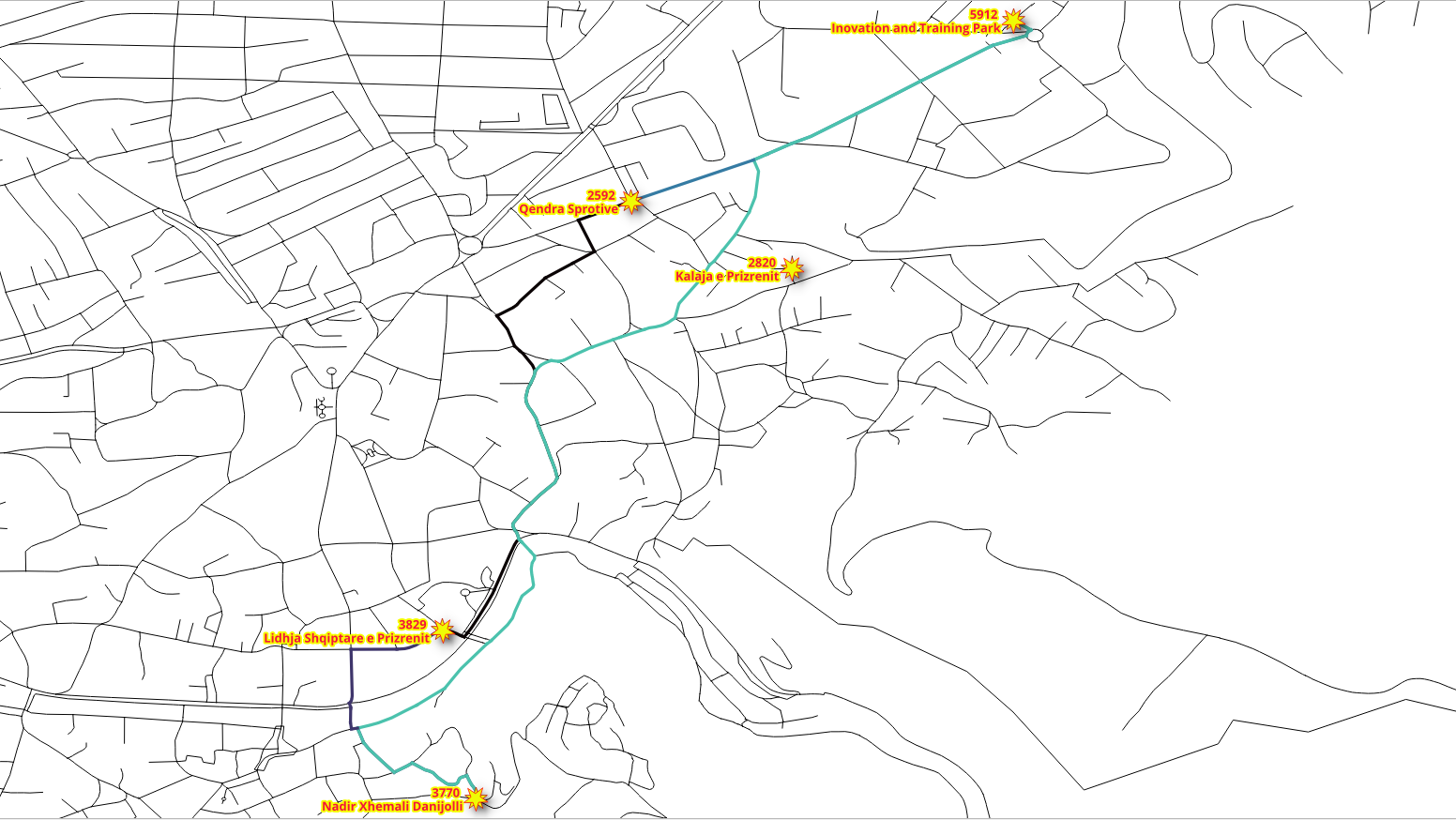
Problem:

Walking
- from “Nadir Xhemali Danijolli” and “Qendra Sprotive”
- to “Inovation and Training Park” and “Lidhja Shqiptare e Prizrenit”
Calculate routes with costs in minutes.

Solution:

The pedestrians depart from 3770 and 2592 (line 9).
The pedestrians want to go to destinations 5912 and 3829 (line 10).
The cost to be in minutes, with a walking speed s = 1.3 m/s and t = d/s (line 6).
Result adds the costs per destination.

SELECT * FROM pgr_dijkstra(
    '
      SELECT gid AS id,
       source,
       target,
       length_m / 1.3 / 60 AS cost
      FROM ways
    ',
ARRAY[3770, 2592],
ARRAY[5912, 3829],
directed := false);

Exercise: 4 (Chapter: Pedestrian)

Note

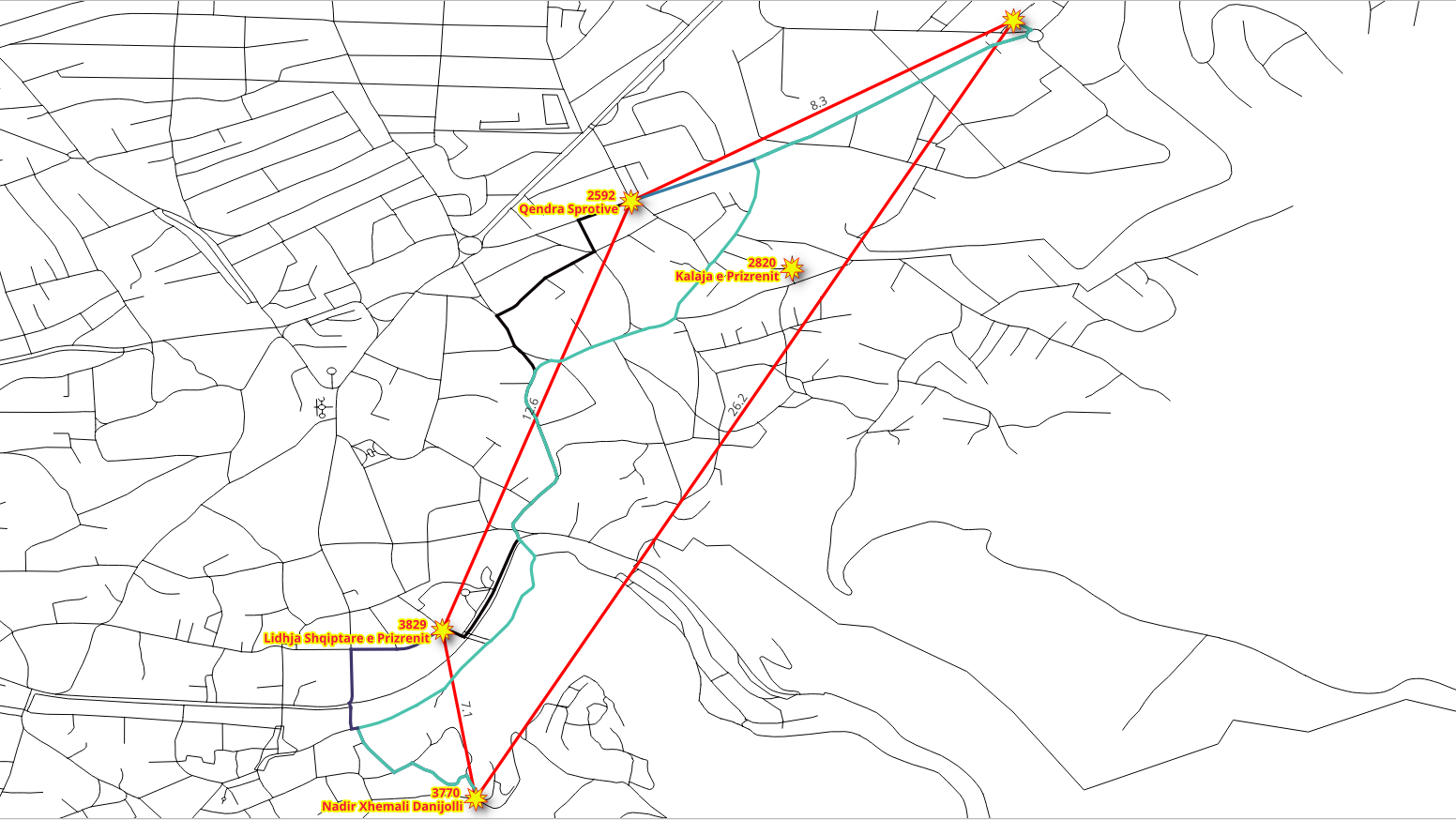
Inspecting the results, looking for totals (edge = -1):

From 3770 to vertex 5912 takes 26.22 minutes (seq = 94)

From 3770 to vertex 3829 takes 7.11 minutes (seq = 48)

From 2592 to vertex 5912 takes 8.31 minutes (seq = 33)

From 2592 to vertex 3829 takes 12.56 minutes (seq = 20)

2.2. pgr_dijkstraCost ¶

When the main goal is to calculate the total cost, without “inspecting” the pgr_dijkstra results, using pgr_dijkstraCost returns a more compact result.

Signature Summary

pgr_dijkstraCost(edges_sql, start_vid,  end_vid  [, directed])
pgr_dijkstraCost(edges_sql, start_vid,  end_vids [, directed])
pgr_dijkstraCost(edges_sql, start_vids, end_vid  [, directed])
pgr_dijkstraCost(edges_sql, start_vids, end_vids [, directed])
pgr_dijkstraCost(edges_sql, combinations_sql   [, directed])

RETURNS SET OF (start_vid, end_vid, agg_cost)
    OR EMPTY SET

Description of the parameters can be found in pgr_dijkstraCost

2.2.1. Exercise 5: Time for many Pedestrians going to different destinations ¶

Problem:

Walking
- from “Nadir Xhemali Danijolli” or “Qendra Sprotive”
- to “Inovation and Training Park” or “Lidhja Shqiptare e Prizrenit”
Get only the cost in minutes.

From the hotels to the |place_4| and |place_5|

Solution:

The pedestrians depart from 3770 and 2592 (line 10).
The pedestrians want to go to destinations 5912 and 3829 (line 11).
The cost to be in minutes, with a walking speed s = 1.3 m/s and t = d/s (line 7).
Result as aggregated costs.

SELECT *
FROM pgr_dijkstraCost(
    '
      SELECT gid AS id,
       source,
       target,
       length_m  / 1.3 / 60 AS cost
      FROM ways
    ',
ARRAY[3770, 2592],
ARRAY[5912, 3829],
directed := false);

Exercise: 5 (Chapter: Pedestrian)

Compare with Exercise 4: Many Pedestrians going to different destinations ‘s note.

2.2.2. Exercise 6: Many Pedestrians going to different destinations summarizing the total costs per departure ¶

Problem:

Walking
- from “Nadir Xhemali Danijolli” or “Qendra Sprotive”
- to “Inovation and Training Park” or “Lidhja Shqiptare e Prizrenit”
Summarize cost in minutes.

Solution:

The pedestrians depart from 3770 and 2592 (line 10).
The pedestrians want to go to destinations 5912 and 3829 (line 11).
The cost to be in minutes, with a walking speed s = 1.3 m/s and t = d/s (line 7).
Result adds the costs per destination.

SELECT start_vid, sum(agg_cost)
FROM pgr_dijkstraCost(
    '
      SELECT gid AS id,
        source,
        target,
        length_m  / 1.3 / 60 AS cost
      FROM ways
    ',
    ARRAY[3770, 2592],
    ARRAY[5912, 3829],
    directed := false)
GROUP BY start_vid
ORDER BY start_vid;

Exercise: 6 (Chapter: Pedestrian)

Note

An interpretation of the result can be: In general, it is faster to depart from “Qendra Sprotive” than from “Nadir Xhemali Danijolli”