5. pgRouting Algorithms¶

5.1. pgr_dijkstra¶

Dijkstra algorithm was the first algorithm implemented in pgRouting. It doesn’t require other attributes than id, source and target ID and cost. You can specify when to consider the graph as directed or undirected.

Signature Summary

pgr_dijkstra(edges_sql, start_vid,  end_vid)
pgr_dijkstra(edges_sql, start_vid,  end_vid,  directed)
pgr_dijkstra(edges_sql, start_vid,  end_vids, directed)
pgr_dijkstra(edges_sql, start_vids, end_vid,  directed)
pgr_dijkstra(edges_sql, start_vids, end_vids, directed)

RETURNS SET OF (seq, path_seq [, start_vid] [, end_vid], node, edge, cost, agg_cost)
    OR EMPTY SET

Description of the parameters can be found in pgr_dijkstra.

Identifiers for the Queries

The assignment of the vertices identifiers on the source and target columns may be different, the following exercises will use the results of this query. For the workshop, some locations of the FOSS4G Bonn event are going to be used. These locations are within this area http://www.openstreetmap.org/#map=15/50.7101/7.1262

SELECT osm_id, id FROM ways_vertices_pgr
    WHERE osm_id IN (33180347, 253908904, 332656435, 3068609695, 277708679)
    ORDER BY osm_id;
    osm_id   |  id
 ------------+-------
    33180347 | 13224
   253908904 |  6549
   277708679 |  6963
   332656435 |  1458
  3068609695 |  9224
(4 rows)

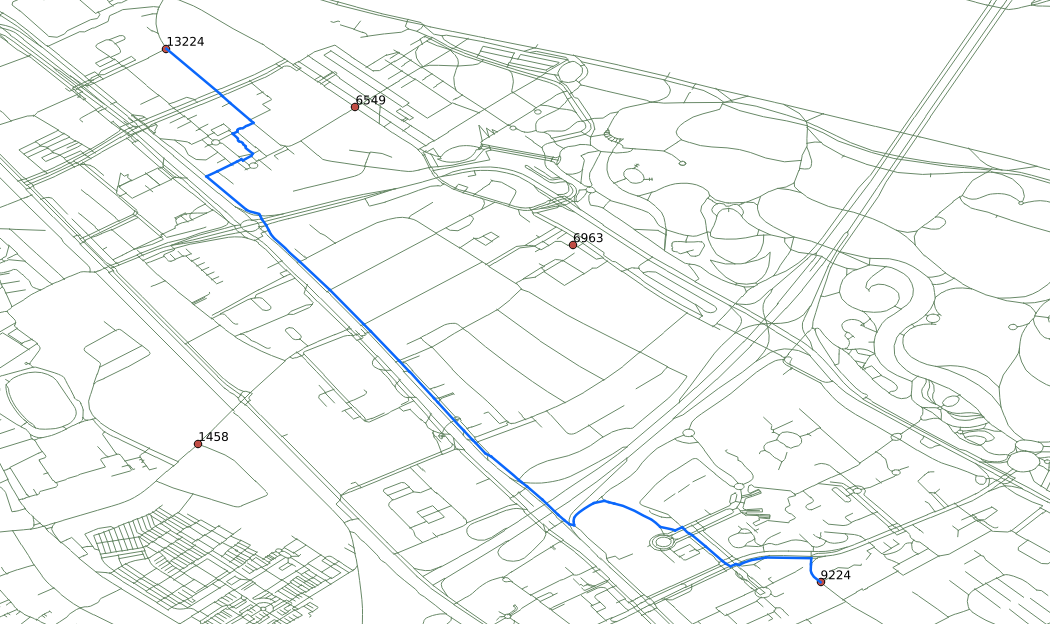
The corresponding id, used in the workshop, and a sample route:

Exercise 1 - “Single pedestrian routing”

• The pedestrian wants to go from vertex 13224 to vertex 6549.
• The pedestrian’s cost is in terms of length. In this case length, which was calculated by osm2pgrouting, is in unit degrees.
• From a pedestrian perspective the graph is undirected, that is, the pedestrian can move in both directions on all segments.

SELECT * FROM pgr_dijkstra('
    SELECT gid AS id,
         source,
         target,
         length AS cost
        FROM ways',
    13224, 6549, directed := false);

Solution to Exercise 1

Exercise 2 - “Many Pedestrians going to the same destination.”

• The pedestrians are located at vertices 6549, 1458 and 9224.
• All pedestrians want to go to vertex 13224.
• The cost to be in meters using attribute length_m.

SELECT * FROM pgr_dijkstra('
    SELECT gid AS id,
         source,
         target,
         length_m AS cost
        FROM ways',
    ARRAY[6549, 1458, 9224], 13224, directed := false);

Solution to Exercise 2

Exercise 3 - “Many Pedestrians departing from the same location”

• All pedestrians are starting from vertex 13224.
• The pedestrians want to go to locations 6549, 1458 and 9224.
• The cost to be in seconds, with a walking speed s = 1.3 m/s and t = d/s

SELECT * FROM pgr_dijkstra('
    SELECT gid AS id,
         source,
         target,
         length_m / 1.3 AS cost
        FROM ways',
    13224, ARRAY[6549, 1458, 9224], directed := false);

Solution to Exercise 3

Exercise 4 - “Many Pedestrians going to different destinations.”

• The pedestrians are located at vertices 6549, 1458 and 9224.
• The pedestrians want to go to destinations 13224 or 6963.
• The cost to be in minutes, with a walking speed s = 1.3 m/s and t = d/s

SELECT * FROM pgr_dijkstra('
    SELECT gid AS id,
         source,
         target,
         length_m / 1.3 / 60 AS cost
        FROM ways',
    ARRAY[6549, 1458, 9224],
    ARRAY[13224, 6963],
    directed := false);

Solution to Exercise 4

5.2. pgr_dijkstraCost¶

When the main goal is to calculate the total cost, for example to calculate multiple routes for a cost matrix, then pgr_dijkstraCost returns a more compact result.

Signature Summary

pgr_dijkstraCost(edges_sql, start_vid,  end_vid)
pgr_dijkstraCost(edges_sql, start_vid,  end_vid,  directed)
pgr_dijkstraCost(edges_sql, start_vid,  end_vids, directed)
pgr_dijkstraCost(edges_sql, start_vids, end_vid,  directed)
pgr_dijkstraCost(edges_sql, start_vids, end_vids, directed)

RETURNS SET OF (start_vid, end_vid, agg_cost)
    OR EMPTY SET

Description of the parameters can be found in pgr_dijkstraCost

Exercise 5 - “Many Pedestrians going to different destinations returning aggregate costs.”

• The pedestrians are located at vertices 6549, 1458 and 9224.
• The pedestrians want to go to destinations 13224 or 6963.
• The cost to be in minutes, with a walking speed s = 1.3 m/s and t = d/s
• Result as aggregated costs.

SELECT *
FROM pgr_dijkstraCost('
    SELECT gid AS id,
         source,
         target,
         length_m  / 1.3 / 60 AS cost
        FROM ways',
    ARRAY[6549, 1458, 9224],
    ARRAY[13224, 6963],
    directed := false) ORDER BY end_vid;

Solution to Exercise 5

5.3. pgr_astar¶

A-Star algorithm is another well-known routing algorithm. It adds geographical information to source and target of each network link. This enables the routing query to prefer links which are closer to the target of the shortest path search.

Signature Summary

pgr_costResult[] pgr_astar(sql text, source integer, target integer, directed boolean, has_rcost boolean);

Returns a set of pgr_costResult (seq, id1, id2, cost) rows, that make up a path.

Description of the parameters can be found in pgr_astar.

Exercise 6 - “Single Pedestrian Routing with Astar.”

• The pedestrian wants to go from vertex 13224 to vertex 6549.
• The pedestrian’s cost is length, in this case length is in degrees.

SELECT seq, id1 AS node, id2 AS edge, cost FROM pgr_astar('
    SELECT gid::integer AS id,
         source::integer,
         target::integer,
         length::double precision AS cost,
         x1, y1, x2, y2
        FROM ways',
    13224, 6549, false, false);

Solution to Exercise 6

There are many other functions available with the latest pgRouting release, most of them work in similar ways. For the complete list of pgRouting functions see the API documentation: http://docs.pgrouting.org/